Information is all around us. It makes up our thoughts and ideas, who we are, what we do, the knowledge we gain from the books we read, the music we listen to, and the smells we smell. It includes everything we perceive from our senses, as well as everything we don’t. It’s everywhere, just as light or gravity is. And like light or gravity, we can measure information.

Much like we can measure distance using a unit such as meters, or temperature in units such as kelvin or celsius, there is a fundamental unit for measuring information. This unit is named bits.

What is a bit?

A bit is nothing more than the answer to a yes or no question. A smoke signal is an example of transmitting 1 bit of information. It answers the question “Is anyone in this location?”. No smoke = no. Smoke = yes. Through inductive reasoning and well-understood conventions, we attribute smoke in a remote location to someone asking for help, but the information which is transmitted is that someone is here.

Because a bit has two possible states (yes or no), you will often see alternative representations such as true or false. Or the number symbols 1 or 0. There are many forms bits of information can take, such as a beep or silence, or an electrical signal with a high or low voltage, or a flag being raised or lowered.

From the bit, we can describe anything and everything around us. One of my favorite childhood games called “Guess Who?” describes what I mean by this.

Guess who is a two-player guessing game where each player selects a card containing a cartoon character. Each player has boards with all 24 possible cartoon characters that make up the deck of cards. Players will take turns asking yes or no questions - for example: 'Does the person on your card have orange hair?' The other player will answer yes or no, then the person asking the question will flip all the faces down on their board to narrow down the possible characters that the other player has for their card. After enough questions have been asked, you can narrow down what character the other player has for their card and win the game. Each time a player takes a turn in the game, they are provided with 1 bit of information.
Guess who is a two-player guessing game where each player selects a card containing a cartoon character. Each player has boards with all 24 possible cartoon characters that make up the deck of cards. Players will take turns asking yes or no questions - for example: 'Does the person on your card have orange hair?' The other player will answer yes or no, then the person asking the question will flip all the faces down on their board to narrow down the possible characters that the other player has for their card. After enough questions have been asked, you can narrow down what character the other player has for their card and win the game. Each time a player takes a turn in the game, they are provided with 1 bit of information.

The word bit is often associated with computers and technology, however, this hasn’t always been the case as you can see from the examples above. Computers (and anything else) indeed communicate information that can be represented as bits. But how are they able to make sense of all these yes’s or 1’s and no’s or 0’s? Perhaps more importantly, what yes/no questions are they asking each other? It’s pretty interesting stuff, but more interesting is that computers send information without yes/no questions first being asked and the other end still understands what it means. Imagine sending the answers before the questions are asked… how will the other end make sense of this? We use a little trick called encoding.

Encoding Information

Encoding can be thought of as an agreed-upon standard for what yes/no questions are asked, what order the questions occur in, as well as how many yes/no questions are asked. One easy to understand example of encoding is the standard known as Morse Code which was used to transmit letters. Morse code is encoding which is a continuous stream of yes/no questions that are asked at a constant rate. Each question is asked within one unit of time. A no for each unit of time is silence or empty space. A yes for each unit of time is a dot. A yes for 3 units of time is a dash. Each unit of time is 1 bit.

So from this, we can understand that to send the letter A from morse code, we would send “10111” this is because there is a dot (1 bit - yes), then we need a space between parts of the same letter (1 bit - no), then we need a dash (3 bits - yes, yes, yes). We could say that the letter A in morse code is 5 bits of information. Another example is to send the word “hi”, it would be “10101010000000101”. The word “hi” in morse code requires 17 bits of information.

We say this information is encoded because we use an agreed-upon standard. Both ends, the transmitter, and the receiver have agreed that the letter A is equivalent to “10111”. Encoding information like this allows us to efficiently send information without the other side needing to ask open-ended questions first. Without encoding, the scenario would be pretty bleak, and might end up looking something like this:

  1. Is it an “A”? - No
  2. Is it a “B”? - No
  3. Is it a “C”? - No
  4. Is it a “D”? - No
  5. Is it an “E”? - No
  6. Is it an “F”? - No
  7. Is it a “G”? - No
  8. Is it an “H”? - Yes

H

  1. Is it an “A”? - No
  2. Is it a “B”? - No
  3. Is it a “C”? - No
  4. Is it a “D”? - No
  5. Is it an “E”? - No
  6. Is it an “F”? - No
  7. Is it a “G”? - No
  8. Is it an “H”? - No
  9. Is it an “I”? - Yes

Hi

Not only does the other end need to ask all these questions, but they need to think of what questions need to be asked to get to the answer they’re looking for. To send individual symbols such as letters, it’s not much of a problem, but still inefficient.

Without encoding, a larger problem occurs when trying to transmit a whole idea, such as in the game Guess Who? The game protects the player by giving them a known number of possible characters on a gameboard which can be flipped up or down. The situation is a lot different when an eyewitness describes the appearance of a criminal to an artist. The artist may be asking questions, and arrive at an answer - but perhaps didn’t ask all the questions required to get the best depiction of the criminal. Encoding provides discrete answers that have well-understood meaning and allows us to save time and accuracy by having a fixed number of possible outcomes without needing to ask the questions upfront.

It may seem like Morse code is arbitrarily assigned dots and dashes. It is true that encoding allows us to arbitrarily assign meaning however it also enables us to optimize efficiency if we take a more calculated approach to assigning meaning.

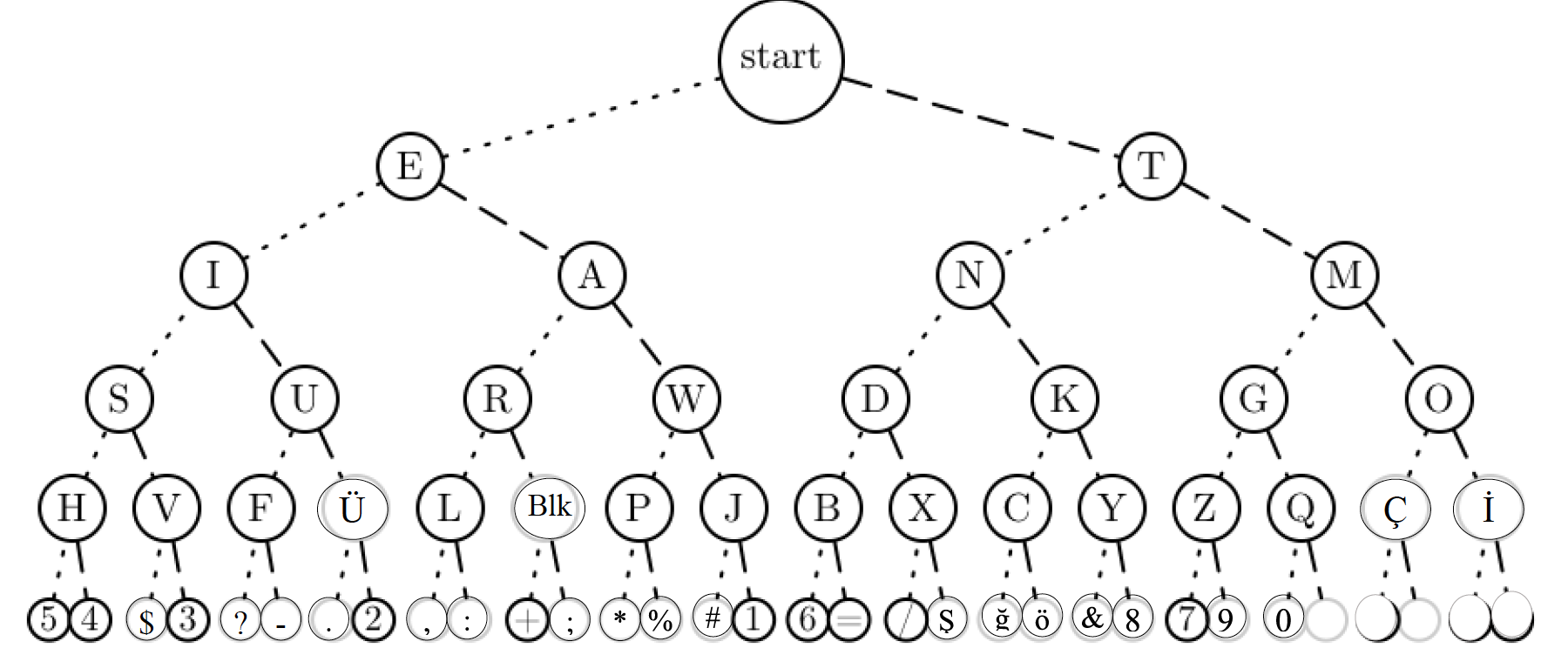
This is the Morse Code Decision Tree. It describes the questions that get asked in order to arrive at a result in order to interpret the message for each symbol. We start at the top and first ask, is this a dot or a dash. If it's a dot, we move left, if it's a dash we move right. We repeat this process until we encounter three time-units of silence (end of the letter, start of the next letter).
This is the Morse Code Decision Tree. It describes the questions that get asked in order to arrive at a result in order to interpret the message for each symbol. We start at the top and first ask, is this a dot or a dash. If it's a dot, we move left, if it's a dash we move right. We repeat this process until we encounter three time-units of silence (end of the letter, start of the next letter).

Morse code intentionally puts more common symbols near the top of the decision tree and biases common symbols to the dot side of the tree since a dot is 1 bit and a dash is 3 bits. The tree is arranged in a way that would optimize the number of bits required to send an English communication so that a typical message would take fewer bits to send than if the symbols were randomly assigned meaning with dots and dashes. Fewer bits means more meaning can be described in the message with less information being transmitted. It’s the equivalent of someone giving a concise defition compared to someone ranting on and on using a lot of filler words like I’m attempting to do right now.

It’s important to understand that because of encoding, in most cases you can pull more meaning out of a transmission with the same amount of information being transmitted. This is because we can assign symbols which occur more frequently in our messages to a unique sequence of yes’s and no’s (1’s and 0’s) with fewer bits. Overall this will reduce the information required (fewer bits) to define our complete message. It’s free and efficient - some of the more common letters in Morse Code are shorter to transmit! This isn’t always the case, but it’s a property gained from encoding which can be used in the design of your code standards.

Wow! Isn’t encoding neat?

Line Code

Nowadays, more modern and widely adopted communication standards such as Ethernet as well as physical standards such as 10GBASE-SR dictate how we exchange information. 10GBASE-SR is a standard used to send ethernet communications at 10,000,000,000 bits every single second! That’s crazy fast, but there are standards which communicate at even faster rates. Of course to send and receive traffic at such a fast rate, we need to use precise clocks on both ends which synchronize up in order to make sense of the messages that get sent. 10GBASE-SR defines what types of lasers are used, what size the module casing for the laser is what how it connects to switches and cables. It also defines the type of cables which must be used and under what circumstances. Last but certainly not leaset, it also defines the line coding, sometimes referred to as the physical coding sublayer. Line coding is important for engineering reasons which I’ll discuss below - but what it does is taken our encoded message, then encode it again following another set of rules.

As mentioned above, clocks on both ends of the line need to be synchronized so they understand how long a time unit, and when a time unit begins or ends. The way the clocks stay in sync is by looking for changes in voltage or light

Closing Thoughts

We often take communications technology in the world around us for granted without thinking too much about what’s going on to make things happen. I find it incredibly interesting that all information around us is transmitted using discrete yes/no questions and answers. If you’re interested in learning more about Information Theory, I’d recommend Khan Academy’s short course on the subject which covers more basic concepts such as what I’ve described here.